这一节我们介绍决策表,按照 IEEE 软件工程知识体系结构的介绍,决策表可以准确地反映程序的输入与输出之间的逻辑关系。我们看这样一个例子,一个关于读书状况的决策表:
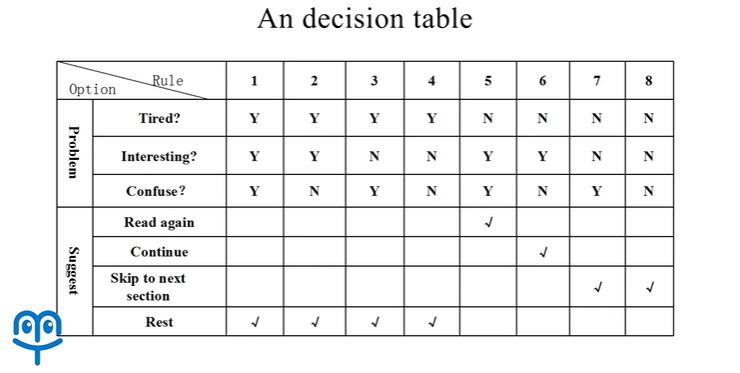
在读书时你觉得累吗?你能理解书本的内容吗?有兴趣吗?那么根据不同的情况组合,我们可以给出如下的不同建议,继续往下读,重新读一遍,休息,以及跳到下一章。
例如大家都接触过布尔逻辑当中的增值表,这其实也是一种决策表:
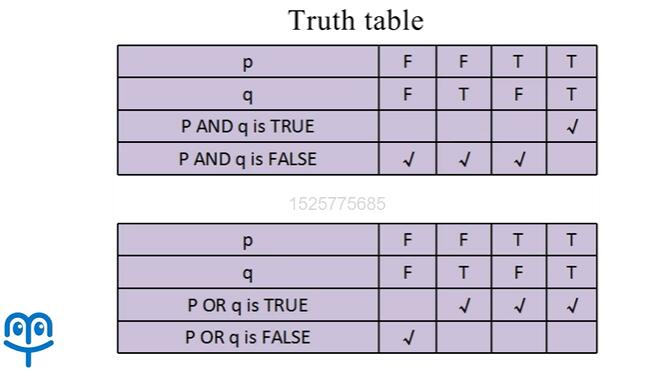
那么这种决策表它可以准确地反映输入与输出之间的逻辑关系,可以帮助我们准确的设计测试用例来检测程序是否满足输入与输出之间应该满足的那些关系:

尤其是对于一些复杂的系统来说,我们可以比较好的检测它们的规格说明。
1.2 决策表的构成
一个决策表,它有以下 4 个部分构成:
- 条件的列表
- 动作的列表
- 条件项
- 动作项

那么在条件项和动作项当中,每一列是由若干个条件的取值以及所对应的动作所组成的。那么这样的一列我们就称之为一条规则。
1.3 如何构造决策表
在构造一个决策表时,我们有以下 5 个步骤:
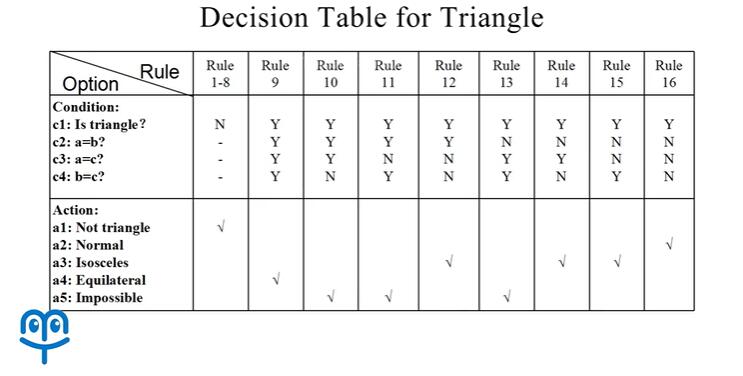
- 首先我们要计算一下规则的数量,如果决策表当中有 n 个条件,那么规则的数量就是 2的 n 次方,2 的 n 次方就是相当于所有条件组合的数量;
- 第二步我们可以列出所有的条件,以及所有的动作;
- 之后填写条件项,所有条件取值的情况全部列出来。注意我们需要 2 的 n 次方列;
- 在对应的每一列当中,我们选择应有的动作,也就是填充完成动作项;
- 最后我们可以对已经得到了这样一个决策表进行化简。

那么对这样一个决策表进行化简时,我们可以合并其中的一些列,也就是合并一些规则,对于有一些规则,相似的条件取值导致了相同的结果。那么这样一些列我们就可以把它作为相似的规则加以合并,这些规则当中对应的那些条件,我们可以用一些符号来进行标记。
例如在三角形程序的决策表当中,我们一开始计算规则的数量,知道规则的数量应该是 2 的 4 次方,而此后我们通过分析发现,规则一到规则八都是相似的,所以我们可以将规则一到规则八合并,最后得到 9 条规则,进而设计 9 条测试用例,这样这 9 条测试用例就可以用来检测三角形程序是否满足设计的需求。