1. 控制流图的概念
1.1 数学图的类比
首先我们来回顾一下数学上图的概念:
一个图 G 由两个集合构成:
- V:有限非空的节点集合
- E:边的集合,连接节点之间的关系
一个可执行程序 P 也可以被表示为:
- S:有限非空的语句集合(程序中的语句)
- F:语句之间的执行关系(控制流)
基于这样的思想,我们可以将一段程序以及这段程序当中语句与语句之间的执行顺序抽象为一个有向图,我们称之为控制流图。
✅ 结论:程序可以被抽象为一个有向图,即控制流图(CFG)
1.2 控制流图的特殊节点
下面来看两个简单的控制流图的例子:
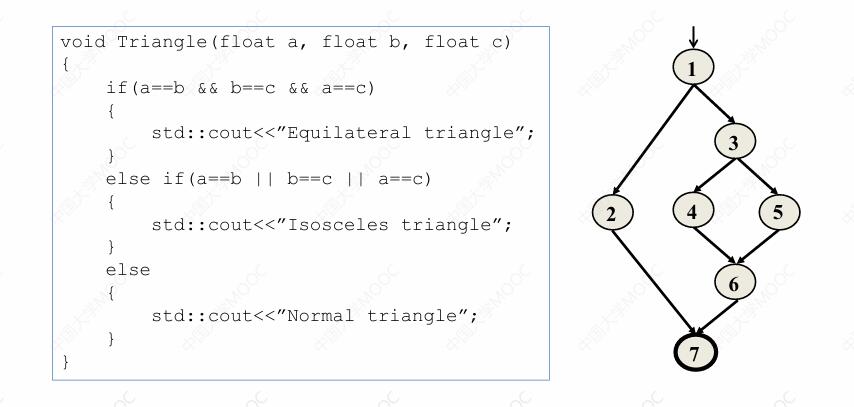

我们注意到在控制流图当中有两类特殊的节点,其中一类节点我们称之为起始节点,在控制流图当中会有一个没有起点的箭头指向起始节点,它用来表示程序的执行入口,在整个程序当中程序的执行入口是唯一的,所以在控制流图当中,起始节点也是唯一的。
另外一类特殊的节点我们称之为终止节点。在控制流图当中,我们会将这样的节点加粗表示它表示程序的执行出口。对于一段程序来说,它的执行出口点并不是唯一的,即终止节点不一定唯一。
✅ 结论:
- 控制流图当中会有一个没有起点的箭头指向起始节点,起始节点唯一
- 控制流图当中加粗的圆表示终止节点,终止节点不一定唯一
2. 三种基本控制结构
我们知道程序有三种基本的控制结构,它们分别是顺序结构,分支结构和循环结构,其中分支结构又分为单项分支结构,双项分支结构和多项分支结构这三种。而循环结构可以分为 while 循环和 until 循环这两种。
2.1 顺序结构
顺序结构是指程序当中既没有分支,也没有循环。我们看这样一段程序,它用来交换 x 和 y 这两个整数。在这段程序当有 4 条语句,我们分别用 1、2、3、4 这 4 个节点来表示这 4 条语句,语句按照顺序依次执行,所以说在控制流图当中会体现出从 1→ 2 → 3 → 4 的这样的执行序列。

2.2 单项分支结构
单项分支当中只有 if 而没有与之对应的 else。我们看这样一段程序,这段程序会从 x 和 y 这两个整数当中找出最大的那一个,然后作为返回值来返回这段程序当中。

我们将 if (x > y) 抽象为控制流图中的节点 1,将 temp = x 抽象为节点 2,将 return temp 抽象为控制流图当中的节点 3.。
当 if (x > y) 为真时,会执行 temp = x,在控制流图当中体现为从 1 → 2 的这样一条边,当 temp = x 执行结束之后,接下来会执行 return temp 这样一条语句,体现为控制流图当中从 2 → 3 的这样一条边。
那么如果 if (x > y) 的条件不满足,会直接执行 return temp 这样一条语句,体现为控制流图当中,从 1 → 3 的这样一条边。
2.3 双向分支结构
双向分支结构当中,if 和 else 语句会成对出现。我们看这样一段程序,这段程序的功能同样是将 x 和 y 这两个整数进行比较,然后选出当中最大的一个数返回。

在这样一段程序当中,if (x > y) 这条语句,用控制流图当中的节点一来抽象。 temp = x 这条赋值语句,用控制流图当中的节点 2 来抽象。 temp = y 这条语句,用控制流图当中的节点 3 来抽象。最后 return temp 语句用节点 4 来抽象。
在这样一个程序当中,如果 if (x > y) 为真,那么会执行 temp = x 的这条语句,在控制流图当中体现为 1 → 2的这条边。如果上述条件不成立,会执行 temp = y 的赋值,在控制流图当中体现为从 1 → 3 的这样一条边。无论条件成立与否,程序最终都会执行 return temp 这条语句。那么我们会看到在控制流图当中,从节点 2 和节点 3 都各有一条边指向节点 4。
2.4 多项分支结构
多项分支结构一般体现为 switch case 这样的代码,下面一段程序用来将百分制的成绩转化为等级制的成绩。
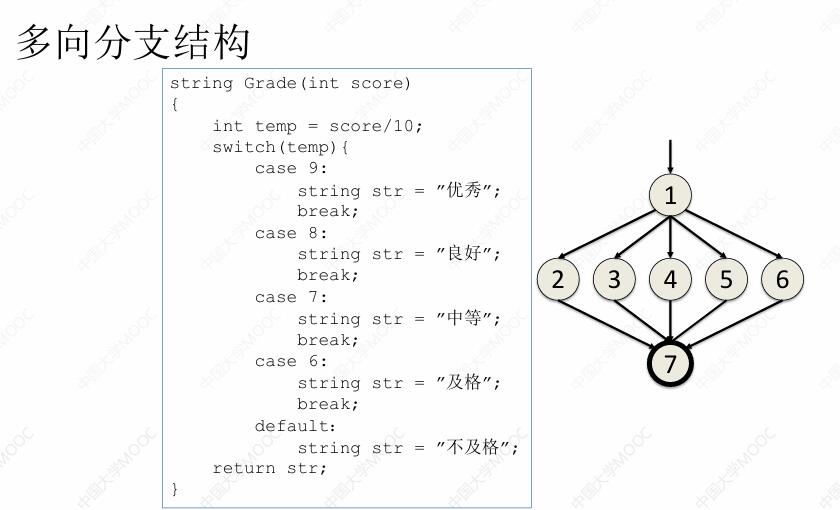
在这段程序当中,我们将 switch 语句抽象为控制流图当中的节点 1,将 case 以及 default 条件下的语句抽象为控制流图当中的 23456,将最后的 return 语句抽象为控制流图当中的节点 7。
这样我们在控制流图当中可以看到,根据 temp 值的不同,程序可以执行不同的 case,从 1 → 2 到 1 → 6,最终不管是哪个分支执行结束之后,都会回到 return 语句上面来。
❓思考一个问题:
如果在这样的程序当中,漏写了每一个 case 条件下的 break,控制流图又会变成什么样子?
2.5 while 循环结构
while 循环结构是指在执行循环体之前,会首先进行循环控制条件的判断,如果循环控制条件为真,则会执行循环体,如果循环控制条件为假,则会跳出循环 。我们看这样一段代码,它的功能是将一个容器当中的元素进行累加
[
这里我们将 while 语句抽象为控制流图当中的节点 1,将循环体抽象为控制流图当中的节点 2,将 return sum 语句抽象为控制流图当中的节点 3。如果条件判断为真,则会执行循环体,在控制流图当中就会体现为从节点 1到节点 2 的这样一条边。
那么节点 2 执行完毕之后,会回到节点 1 进行下一次判断。那么当判断结果为假时,控制流图当中就会出现 1 → 3 这样一条边表示跳出循环。
2.6 until (do-while) 循环结构
until 循环结构一般用在循环体至少会执行一次的场景下。这时循环体首先会进行第一次执行,然后进行循环控制条件的判断,如果循环控制条件为真,则循环体进行下一次的执行,否则则会跳出循环结构。我们看这样一段代码,它同样是对一个 vector 容器当中的元素进行累加,这里我们使用 assert 语句来确保容器当中的元素数量至少是有一个。

我们将这段程序当中的循环体抽象为控制流图当中的节点 1,将 while 语句抽象为节点 2,将 return sum 语句抽象为节点 3。在执行完 assert 语句以及一些变量的初始化操作之后,循环体会进行第一次执行,体现为控制流图当中的节点 1,然后会进行循环控制条件的判断,体现为控制流图当中从 1 → 2 的这样一条边,那么如果这个循环控制条件为真,则会从节点 2 跳转到节点 1 表示执行下一次循环体。如果循环控制条件为假,则会从节点 2 跳转到节点 3 ,表示执行 return sum 语句。
3. 路径
3.1 路径的概念
现在我们已经能够针对几种基本的程序结构来绘制控制流图了。当我们拥有了控制流图之后,我们需要关注一个叫做路径的概念,所谓路径是指一系列节点所构成的一个序列,在这两个序列当中,任意两个相邻的节点必须有边连接 。
那么假设我们现在有一个包含了 7 个节点的控制流图,它包含两个 if else 的双向分支结构。
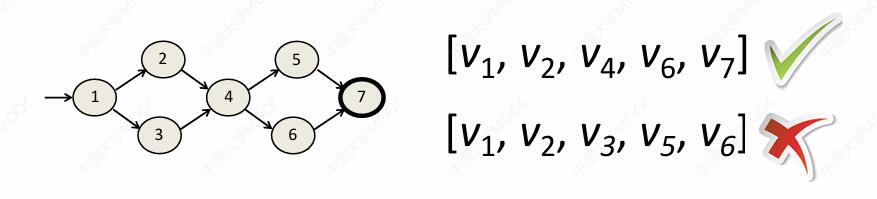
在这样一个控制流图当中,我们可以看到 12467 它会是一条路径,而 12356 它就不是一条路径,为什么?因为从 3 到 5 在控制流图当中并不存在这样一条边。
3.2 测试路径的概念
进一步我们可以来了解一下测试路径的概念。所谓测试路径就是指程序在某一条测试用例下执行时在控制流图当中所形成的这样一条,从起始节点到终止节点的路径 。
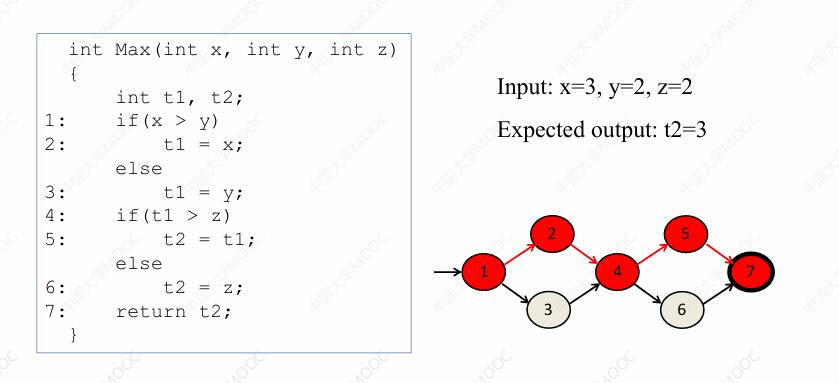
我们考虑这样一段程序,这段程序会将整数 xyz 三者当中最大的值返回。假设我们的测试用例输入是 x = 3,y = 2,z = 2,那么在这条程序当中,它的执行序列会是从语句一到语句二,再到语句四,然后是语句五和语句六,体现为控制流图当中,从 1 → 2 → 4 → 5 → 6 的这样一条测试路径。
4. 总结
| 控制结构 | 图中特征 |
|---|---|
| 顺序结构 | 节点线性连接 |
| 单分支 | 形似三角形 |
| 双分支 | 条件节点分两路,最后归并,形似菱形 |
| 多分支 | switch 节点分多路,最后统一指向 return |
| while 循环 | 条件判断 → 循环体 → 可能回环或终止 |
| do-while | 循环体 → 条件判断 → 可能回环或终止 |