1. 判定语句（Decision Statement）与谓词语句（Predicate Statement）
1.1 判定语句/谓词语句的概念
逻辑测试在程序当中会有这样一类特殊的语句，在这样的语句当中会有一个逻辑判断结果的真与假会决定程序，执行一个分支结构当中的真分支还是假分支，或者是决定程序是否执行循环结构当中的循环体。对于这样的语句，我们称之为判定语句（Decision statements） 或者是谓词语句（Predicate statements）。
由于判定语句或者谓词语句当中的逻辑表达式会直接决定程序的执行流程。所以说在测试当中，我们需要对这一类逻辑判断语句进行重点关注。判定语句与谓词语句当中的逻辑表达式一般都会书写为一个布尔表达式的形式。
1.2 基于布尔表达式输出的判定覆盖准则 DC
我们首先来关注布尔表达式的输出，从而得到一种逻辑覆盖准则（判定覆盖 DC）。
✅关注点：布尔表达式的输出结果（True / False）
✅目标：每个判断表达式的真值和假值都至少出现一次。
在基于判定覆盖的测试中，我们需要设计测试用例，使得测试用例执行后，每一个判定表达式的可能的判定结果均出现。
当我们执行一组测试用例之后，可以针对这组测试用例来计算它的判定覆盖率，其中分子是判定表达式已经得到的输出的数量，而分母是判断表达式所有可能的输出的数量。
✅结论：判定覆盖率 = 已出现的判定结果数量 / 所有判定结果的总数
1.3 判定覆盖的计算示例
我们继续三角形程序的例子，在这个三角形程序当中共有两个判定语句。
首先我们执行第一条测试用例 a = 2，b = 2，c = 2。这个时候第一条，判定表达式当中它的结果为 true，那么这个时候因为共有 2 条判定表达式，也就是共有 4 种可能的输出，所以此时的判定覆盖率是 1/4。
执行第二条测试用例，a = 2，b = 2，c = 3，那么这个时候第一条判定表达式的判定结果为 false，会进入到第二条判定语句的执行。那么这个时候第二条判定语句的判定结果为真，也就是说我们得到了两个新的输出，所以此时累计的判定覆盖率为 3/4。
后我们执行第三条测试用例 a = 2，b = 3，c = 4。那么这个时候第二条判定语句它的判定结果为 false，这个时候两条判定表达式所有可能的判定结果都已经出现，所以此时累计的判定覆盖率是 100 %。
1.4 基于布尔表达式输入的条件覆盖准则 CC
如果我们关注布尔表达式的输入，也可以得到一种逻辑覆盖准则（条件覆盖 CC）。
✅关注点：布尔表达式的输入取值
✅目标：每个布尔条件的 True 和 False 取值都至少出现一次。
也就是在基于条件覆盖的测试中，我们需要设计测试用例，使得测试用例执行后，对于每一个判定表达式当中所有的布尔条件可能的取值均出现。
当我们执行过一组测试用例之后，我们可以针对这组测试用例来计算它的条件覆盖率，其中分子是所有被执行过的判定表达式当中的所有布尔操作数，也就是布尔条件它的取值的数量，而分母是这些判定表达式当中，所有的布尔操作数也就是布尔条件，所有可能的取值的数量。
✅结论：条件覆盖率 = 布尔条件实际取值个数 / 布尔条件所有可能取值总数（2 × 条件数）
1.5 条件覆盖的计算示例
我们继续三角形程序的例子，在这个三角形程序当中共有两个判定语句。
在这样一段程序当中，共有 2个判定表达式，每个判定表达式当中又有 3 个布尔操作数，也就是说会有 12 个取值需要被覆盖。
我们首先执行第一条测试用例 a = 2，b = 2，c = 2，这个时候第一个判定表达式当中的 3个布尔条件，它们的取值都是 true，所以此时条件覆盖率达到了 3/12。
接下来执行第二条测试用例 a = 2，b = 2，c = 3，这条测试用例执行后，第一个判定表达式当中，b = c 和 a = c 这两个布尔条件它们的取值都为 false。而第二个判定表达式当中 3 个布尔条件，第一个 a = b 的取值为 true，第二个 b = c 的取值为 false，第三个 a = c 的取值为 true ，那么累计的条件覆盖率达到了 8/12 .
注意，对于执行的条件语句我们才计算该条件语句提供的条件覆盖率
我们继续执行第三条测试用例，也就是 a = 2，b = 3，c = 4。这个时候第一个判定表达式当中的条件，a 等于 b 取值为 false。而第二个判定表达式当中的 a = b 取值也为 false。那么这个时候又有两个新的条件取值被覆盖，所以此时的累积条件覆盖率达到了 10/12。
第四条测试用例 a = 3，b = 2，c = 2，执行后第二个判定表达式当中的 b = c 的布尔条件取值为真，那么这个时候我们又增加了一种条件的取值，所以总的条件覆盖率达到了 11/12。
之后我们再执行第五条测试用例，a = 2，b=3，c = 2。那么这个时候第二个判定表达式当中的 a = c 的条件取值为真，此时所有 6 个条件当中的 12 个取值全部出现，所以此时的累积条件覆盖率达到了 100%。
2. 条件覆盖 VS 判定覆盖，谁更强？
条件覆盖和判定覆盖分别考虑了布尔表达式的输入和输出，那么这两种覆盖到底哪个更强，哪个更弱？
在刚才的案例当中我们可以看到同样的三条测试用例可以达到 100 %的判定覆盖率，但是在条件覆盖率这里却没有达到 100%，我们需要补充更多的测试用例，才能达到 100% 的条件覆盖率，这也说明判定覆盖肯定不强于条件覆盖。
那么条件覆盖是不是就强于判定覆盖呢？似乎也不是，我们看这样一个例子，那么在这段程序当中程序会接受 x y 这两个输入，如果 x 和 y 都是大于 0 的，x 乘以 y 它就是一个正数。
string Fun(int x, int y){
string str;
if (x > 0 && y > 0)
str = "x*y is positive";
...
return str;
}
那么在这样一段程序当中，我们设计两条测试用例。第一条测试用例 x = 1，y = -1，第二条测试用例 x = -1，y = 1。那么通过这两条测试用例，我们可以使 x > 0 和 y > 0。这两个布尔条件的真假都出现，也就是累积的条件覆盖率达到 100 %。但是很显然这两条测试用例执行之后，if 语句它们的判定结果都是 false，也就是说这个时候条件覆盖率达到了 100%，判定覆盖率并没有达到 100%，也就是说我们不能说条件覆盖比判定覆盖更强。
✅结论：不能简单的说条件覆盖和判定覆盖谁更强
3. 判定条件覆盖 DCC
所以人们就提出了一种整合了判定覆盖和条件覆盖的一种新的覆盖准则，叫做判定条件覆盖（DCC）。那么所谓判定条件覆盖指的就是我们既要实现判定覆盖，也要实现条件覆盖，那么类似的在对这种覆盖率进行计算时，我们需要考虑判定覆盖率和条件覆盖率，这两者需要分别进行计算，计算公式上文已经提到。
4. 条件组合覆盖 CCC
4.1 条件组合覆盖 CCC 的概念
当一个布尔表达式当中有多个布尔条件时，每一个输入变量它的取值都会对最终的判定结果造成影响。所以我们在测试时需要考虑这一些输入变量的取值的组合对最终判定结果的影响。为此人们提出了条件组合覆盖，它也是一种逻辑覆盖准则。
✅关注点：布尔表达式的输出结果（True / False）
✅目标：每个判断表达式的真值和假值都至少出现一次。
在基于条件组合覆盖的测试中，我们需要设计测试用例，使得测试用例执行后，对于每一个判定表达式当中，所有的布尔条件，它的取值组合都出现相应的在执行一组测试用例之后，我们也可以针对这组测试用例来计算它的条件组合覆盖率，其中分子是已经出现过的布尔条件的取值组合的数量，而分母是所有可能出现的布尔条件取值组合的总数量。
✅条件组合覆盖率：已出现的组合数量 / 所有合法组合数（假设布尔条件数为 n，组合数为 2^n）
4.2 条件组合覆盖率的计算示例
我们看这个三角形程序的例子，在这个三角形程序当中共有两个判定表达式，而这两个判定表达式所包含的布尔条件是完全一样的，它们都是 a = b b = c 和 a = c 那么这样我们可以把所有 3个布尔条件一一列出来，同时把它们之间所有可能的取值组合总共是 8 种组合，也都列出来。
针对条件取值组合的每一种情况，我们都尝试去设计测试用例。在这 8 种情况中，我们有 5 种情况是可以设计测试用例的，另外有 3 种情况，我们没有办法设计测试用例。
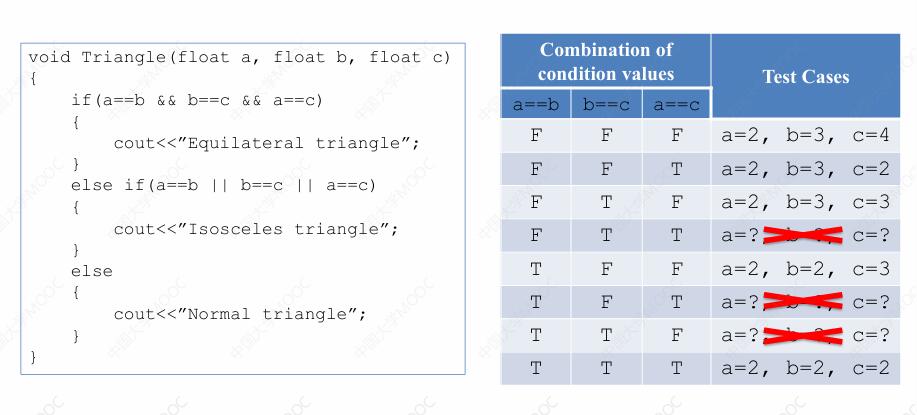
为什么呢？这三种情况当中都是有一个条件，它取值为 false，而另外两个条件取值为 true。那么这也就是意味着在 a = b ` b = c` a = c 这三个条件当中有两个为真，一个为假，而这显然是不可能的，所以说对于这三种情况，我们无法设计测试用例。
5. MC/DC 覆盖
5.1 MC/DC 覆盖的概念
我们来关注单个布尔条件对布尔表达式最终判定结果可能造成的影响，也就是 MC/DC 覆盖。
✅目标：测试用例能够展示单个布尔条件的变化能独立影响整体判定结果。
✅目标：成对设计测试用例，仅一个条件变化，且改变了整体结果。
在基于 MC/DC 的测试当中，我们需要设计测试用例来体现这样一种场景：在成对的两条测试用例当中，某一个布尔条件它的取值变化可以独立的对这条判定表达式的判定结果造成影响。
举个例子，当我们开车时，如果遇到紧急情况，我们踩下刹车，我们希望不管当前汽车处于什么样的状态，那么汽车都必须进行制动的操作。也就是说刹车踏板状态的变化应该能够独立地影响整台汽车的工作状态。
我们可以对一组测试用例计算 MC/DC 覆盖率，它的分子是满足独立影响的布尔条件数量，而分母是布尔条件总数。
✅MC/DC覆盖率： 满足独立影响的布尔条件数量 / 布尔条件总数
5.2 MC/DC 覆盖率的计算示例
在三角形程序的例子中，我们来关注第二个判定表达式，也就是 a = b 或者 b = c 或者 a = c。
注意看以上的四条计算用例，我们通过这 4 条测试用例，体现了 a = b 或者 b = c 或者 a = c 这样一条判定表达式当中的 MC/DC 的效应，从而使得这条判定表达式的 MC/DC 覆盖率达到了 100 %。
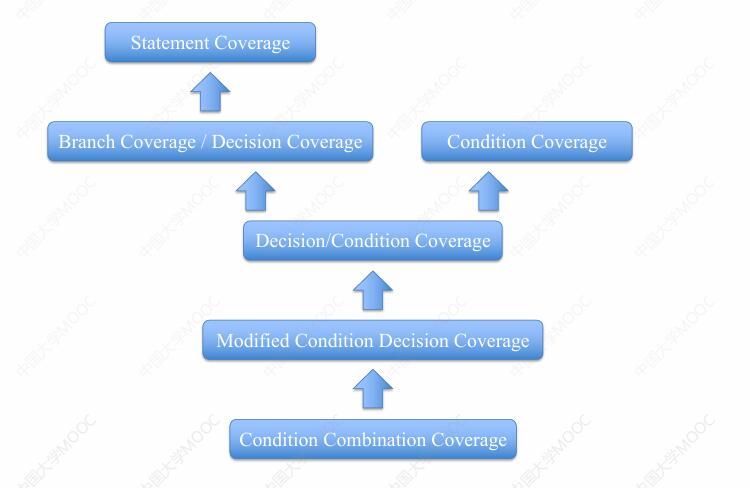
好，以上我们介绍了几种常见的逻辑覆盖准则，那么最终我们可以给出这几种逻辑覆盖准则之间的强弱关系。大家可以思考一下这样一个强弱关系，我们是如何得到的？
