1. 路径覆盖
1.1 路径覆盖的概念
在前面的文章中,我们已经知道,当一条测试用例执行时,在控制流图当中会形成一条从起始节点到终止节点的路径。那么路径覆盖的核心问题就是:我们在测试时是否能够遍历控制流图当中所有可能的从起始节点到终止节点的路径呢?
1.2 路径覆盖的程序示例
在老朋友三角形程序当中,这样做是没有问题的:
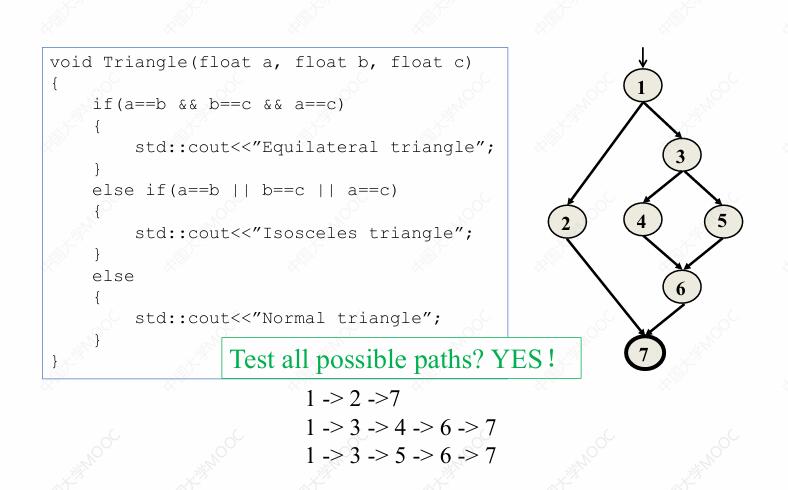
我们可以测试所有可能的路径,因为我们只需要三条路径就可以遍历所有可能的从起始节点到终止节点的路径,它们分别是 :
- 1 → 2 → 7
- 1 → 3 → 4 → 6 → 7
- 1 → 3 → 5 → 6 → 7
这三条路径,但是对于另外一个程序结论可能就有所不同。

在这样一个程序当中,我们读入一个数组,对这个数组进行求和运算,然后再求它的方差。为了遍历这样一个存放了数组的容器 vector,我们需要进行两次循环,那么这两次循环分别用来进行累加操作和求方差的操作。所以在控制流图当中我们可以看到有两个循环结构。
那么这种情况下,我们想要遍历所有可能的路径就是不可能的,为什么?我们可以将所有可能的执行路径,用一个正则表达式的形式来表示出来:
<span class="hljs-number">1</span> → <span class="hljs-number">2</span> → <span class="hljs-number">3</span> (→ <span class="hljs-number">4</span> → <span class="hljs-number">3</span>)* → <span class="hljs-number">5</span> → <span class="hljs-number">6</span> → <span class="hljs-number">7</span> (→ <span class="hljs-number">8</span> → <span class="hljs-number">7</span>)* → <span class="hljs-number">9</span>
容器当中元素的数量不同,会导致循环体执行数量的不同,那么循环体执行次数不同,就会对应不同的执行路径,也就是说我们的主要问题出在了循环上面,因为循环的存在,所以我们没有办法去遍历所有可能的路径。
2.循环路径测试的替代方案
我们的主要问题出在了循环上面,因为循环的存在,所以没有办法去遍历所有可能的路径。那么针对这样一个问题如何解决呢?人们提出了两种方法,第一种方法,我们会借鉴等价类划分的思想来确定循环的次数。而第二种方法是基本路径测试方法。
2.1 等价类划分
我们该如何将等价类划分的思想应用于循环的测试呢?如果我们能够控制循环的执行次数,它的有效等价类和无效等价类分别是什么?或者说它的有效的输入范围是什么?
一个循环体它的执行分为不执行和至少执行一次这两种情况。如果我们能够确定循环体的最大执行次数 max,这个时候我们就得到了两个有效等价类:
| 等价类 | 描述 | 区间范围 |
|---|---|---|
| EC1 | 循环执行 0 次 | {0} |
| EC2 | 循环执行 1 到 max 次 | [1, max] |
第一个有效等价类只包含一种情况,也就是循环执行 0 次。而第二个有效等价类,它的下限为循环执行 1 次,而上限是循环执行 max 次。
我们重点关注第二个有效等价类。首先在 1 和 max 之间取一个中间的数字,标记为 m ,来表示有效等价类,也就是说让循环体执行 m 次。这样我们让循环体分别执行零次和 m 次,就实现了等价类划分的这样一种思想。
2.2 边界值分析
对于边界值分析,我们需要在边界值左右进行滑动,那么 1 向下滑动为 0 ,向上滑动就是 2,而 max 向下滑动是 max-1,向上滑动是 max+1,那么我们就得到了这么 7 种情况:
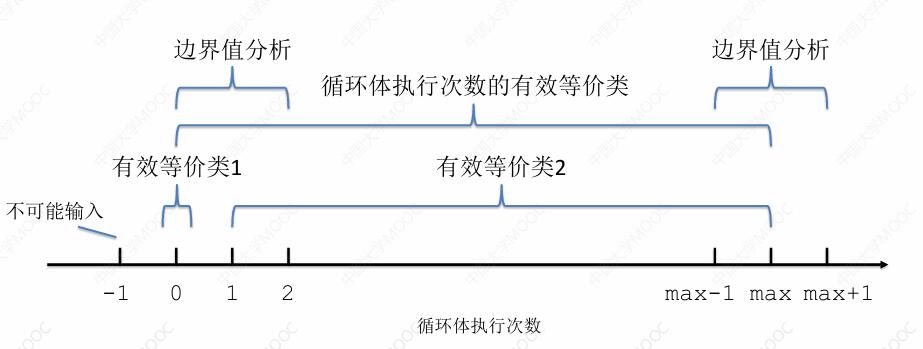
我们设计测试用例让循环体的执行次数分别实现这 7 种情况,这就是如何将等价类划分的思想应用于循环测试:

考虑刚才对 vector 容器当中的元素进行遍历累加,以及求方差操作的这样一段程序:

我们需要设计 7 条测试用例,在这 7 条测试用例当中针对 numbers 这样一个输入,假设我们的测试环境是 32 位系统,它们当中所包含的元素的数量分别应该是 0、1、2、20(可以是别的有效值)、2^32-2、2^32-1 以及 2^32。

那么当 vector 当中元素的数量达到 2^32 的时候,就会发生整数溢出,在这种情况下程序是没有办法正常执行的。而另外 6 条测试用例程序都可以正常的执行,然后会出现 6 种不同的测试路径。