1. 等价类划分

这一节我们介绍等价类划分。我们首先考虑这样一个程序：

float SQRT (float x)
{
    if(x < 0)
        Error;
    else if (x == 0)
        return 0;
    else{
        // computing here
        return result;
    }
}

对于这样一个计算开平方的程序，我们发现：

• 当输入值小于 0 时，我们应该给出一个出错信息；
• 当输入等于 0 时，我们知道 0 的开平方依然是 0，所以应该直接返回结果 0；
• 当输入大于 0 时，我们需要调用一些复杂的算法来计算它的开平方的值。

那么对这样一个软件进行测试，我们至少需要选择三条不同的测试用例，小于 0 的测试用例，等于 0 的测试用例，以及大于 0 的测试用例，这就是等价类划分的基本思想。

1.1 等价类划分的定义与划分标准

所谓等价类划分，我们按照一定的标准对输入域进行划分，将其划分为一个个子集，然后在每个子集当中去选择一些有代表性的测试用例来进行测试。

在对输入域划分时，我们有以下一些原则：

• 可以根据程序对于不同类型数据的处理来进行划分；
• 可以根据不同的数据所拥有的控制流以及数据流的情况来进行划分；
• 可以最简单的根据数据合法非法与否来进行划分。

我们尤其要注意在进行等价类划分时，一般需要同时考虑合法输入和非法输入。所谓合法输入主要是用来检测程序的功能，而非法输入主要用来检测程序是否能够实现合适的错误处理情况。

1.2 等价类划分的两个基本原则

在进行等价类划分时，我们要注意以下两个基本的原则，完备性原则和无冗余性原则：

• 完备性要求我们在进行等价类划分时：
  • 输入域当中的任何一个点，或者任何一个区域都至少要属于一个等价类
  • 输入域当中不能有任何点，它不属于任何等价类
• 无冗余性是指任意两个等价类之间不应该存在交集。

1.3 等价类划分的方法

首先我们可以按照输入数据的范围来进行划分，对于一个输入数据，假如我们指定了它的输入范围，那么这个时候可以划分出一个有效等价类和两个无效等价类。

例如这里有一个程序，它要求输入大于 10 小于 100 的整数，这个时候可以划分出一个有效等价类，也就是输入大于 10 小于 100 以及两个无效等价类，分别是输入小于等于 10 以及输入大于等于 100。

此外我们还可以按照程序对于不同类型数据的不同处理情况来进行划分。如果程序接受 n 种不同的数据，而对这 n 种不同的数据，有 n 种不同的处理方式，那么这个时候我们可以划分出 n 个有效等价类以及 1 个无效等价类。

例如有一个程序它的输入变量 x 可以是 1,3,7,15 当中一种。程序对这 4 种不同的数据做不同的处理。那么这个时候我们可以划分出 x 等于 1，x 等于 3，x 等于 7，x 等于 15， 4 个有效等价类以及 1 个无效等价类，也就是 x 不等于 1,3,7,15 的情况。

此外我们还可以按照输入的条件来进行划分，假如输入指定了一个条件，那么这个时候我们可以划分出一个有效等价类和一个无效等价类。

假如我们要求程序输入一个奇数，那么我们可以划分出一个有效等价类，也就是所有的奇数。以及一个以及一个无效等价类，也就是所有的非奇数。将这条规则扩展，我们还可以根据多种条件来进行划分：假如一个输入变量需要同时满足多个条件，那么我们可以划分出一个有效等价类和 n 个无效等价类。

例如程序要求输入一个字符串，这个字符串它的长度必须是 8，需要以字符 a 打头，并且只能包含小写的 a 到小写的 z 之间的这样一些字符，那么这个时候我们可以设置一个有效等价类，他同时满足所有三个条件，另有三个无效等价类，分别从三个不同的角度来违反规则：

注意，这一条在 2023 年试卷里面考过。

2. 边界值分析

2.1 为什么要做边界值分析

等价类划分法的不足：如果我们在每个等价类中随机选取测试用例，可能会错过边界错误。我们看这样一个例子：

在这个例子当中程序出现了错误：x < 0 的判断被我们错误的写成了 x <= 0。这样当输入等于 0 时，本来应该有的输出 0 被出错信息所替代。

为了检测这样一条错误，我们需要输入等于 0 的这样一条测试用例。按照此前所讲的等价类划分方法，我们对这一程序进行等价类划分，按照输入的有效与否，我们可以划分出一个有效等价类和一个无效等价类，无效等价类对应 x < 0，有效等价类对应 x >= 0。

我们在这两个等价类当中可以随机的选择两条测试用例。那么如果这两条测试用例当中不包含 x = 0 的测试用例，上述的错误我们就没有办法检测到。

所以我们不仅选取等价类的代表值，还要选择接近边界的值来测试。考虑两个等价类之间的边界，就会发现对于第一个等价类，它的边界是 0 和一个非常小的负数。第二个等价类的边界是 0 和一个非常大的正数。

如果我们既考虑两个等价类的代表值，也考虑两个等价类的边界，我们就可以使用这 5 条测试用例来进行测试。这 5 条测试用例一方面覆盖到了两种等价类，另一方面也考虑了两个等价类之间可能的边界，也保证了能够检测我们刚才所提到的那样一个错误。

2.2 如何做边界值分析？

进行等价类划分之后应该如何进行边界值的分析呢？假设这个时候我们已经拥有了一个等价类的范围，是 [min, max]，则应选取如下值进行测试

• 代表性中间值（典型等价类值）
• min (边界值)
• min + 1（略大于最小值）
• max - 1（略小于最大值）
• max（边界值）

例如对于这样一个程序，它有 x1 和 x2 两个输入，那么对它进行等价类划分之后，再进行边界值分析。我们所需要考虑的测试用例如这张图所示，总共需要考虑 9 条测试用例：

那么在这样一个例子当中，大家可能会发现我们没有考虑非法输入，也就是说没有考虑程序可能需要处理错误输入的情况。如果我们考虑非法输入的话，我们需要增加一些数据：

• min - 1（非法最小值）
• max + 1（非法最大值）

3. 随机测试

3.1 随机测试的定义

我们首先看一下 IEEE 软件工程体系结构对于 Random Testing 的定义。在这一文档当中要求我们首先定义程序的输入域，之后在程序的输入域上随机的去选择一些点来作为测试用例，那么这种随机测试方法比较方便实现测试的自动化。

接下来我们看这样一个简单的例子：接受 ab 两个输入参数，ab 相加之后，它的返回值就是 Add() 的运行结果。

int Add (const int &a, const int &b)
{
    return a+b ;
}

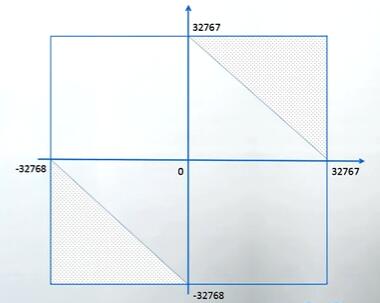
如果这些系统是 16 位的系统，那么我们知道一个 int 类型，它的输入域应该是 -32768 ~ 32767。那么相应的， Add() 的函数，它的输入域就可以作为这样一个矩形，我们在这样一个矩形当中去任意的选择一些点，就可以实现随机测试。

3.2 随机测试面临的问题

随机测试尽管比较简单，但我们在使用随机测试时也可能会面临一些问题，首先是程序输入域的定义，我们首先需要详细分析文档，然后选择合适的输入域。

其次我们可能还会面临随机数生成的问题。众所周知，在计算机系统当中，我们很难得到真正的随机数作为替代的方法。我们可以采用一些伪随机数的生成算法，比如经典的平方取中法，那么在使用这些伪随机数生成算法时，还需要注意，我们一般需要给定一个合适的随机数种子。

3.3 模糊测试

最后我们再介绍一种比较特殊的随机测试技术 — 模糊测试（Fuzzing testing）。模糊测试技术可以看作是随机测试技术的一种特殊应用，主要应用于软件安全性测试领域。在模糊测试当中，我们需要构造一些非法的输入去攻击软件，使得软件发生崩溃。

3.4 自适应随机测试

之前我们了解了随机测试技术，随机测试技术非常简单，但我们在使用随机测试技术时，由于不考虑任何其他类型的信息，这样可能会导致错误检测效率的降低。我们考虑程序当中可能存在的一些特性：

例如对于这样一个程序：

int Add (const int &a, const int &b)
{
    return a+b ;
}

如果这一程序运行在 16 位的系统上，a 和 b 2 个整数相加的结果超出 16 位的话就会发生整数溢出。我们观察这个程序的输入域，就会发现所有能够导致整数溢出的输入，全部集中于输入域的左下角和右上角，这一现象提示我们在软件测试当中导致程序出错的测试用例可能存在聚集的特性。

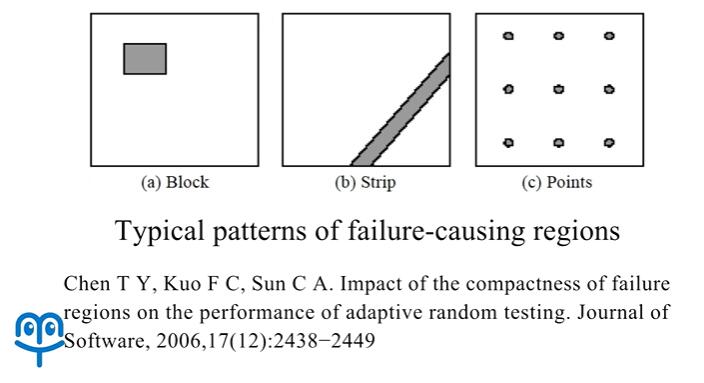
此前已经有科学家对这一现象进行了总结，能够导致程序出错的测试用例，被归结为矩形状分布，条带状分布以及散点状分布这么几种类型。那么对于矩形状分布和条带状分布来说，我们就可以利用测试用例的这种聚集特性来提高随机测试的效率。

如果一条测试用例运行通过，那么在它的附近其他测试用例运行通过的可能性也会比较大。如果有一条测试用例运行失败，在它的附近其他测试用例运行失败的可能性也比较大，这就给我们一种提示，在随机测试当中，每次选择测试用例时，我们可以到尽可能远的地方去选择，就是自适应随机测试（Adaptive Random Testing, ART）的思想。

我们可以首先选择第一条测试用例，如果这条测试用例没有发现任何错误，那么我们定义一个距离 d1，寻找下一条测试用例时就到离第一条测试用例大于这个距离的地方去寻找。如果第二条测试用例依然没有发现错误，就定义一个距离 d2，寻找第三条测试用例时，要求距离前两条测试用例的距离大于 d2，以此类推还可以去寻找第三条，第四条测试用例，直至在输入域当中发现错误。

ART 思想的一种最基本的算法，叫做固定候选集的自适应随机测试算法，简称为 FSCS-ART。

在这一算法当中：

• 首先我们随机生成第一条测试用例，之后如果测试终止条件不满足，注意这里所说的测试终止条件可能是寻找到一条错误，也可能是测试资源耗尽。
• 那么如果测试终止条件没有满足，我们在选择下一条测试用例时，首先随机生成 k 个候选测试用例之后，对于每一个候选测试用例计算它与此前已有测试用例的距离，我们从这些候选测试用例当中去选择一条测试用例，使得它与已有的测试用例具有最大的距离。
• 运行这套测试用例。以此类推，直到测试终止条件满足。

自适应随机测试技术可以有效地提高软件测试的效率，加快我们发现错误的速度，但是在使用自适应随机测试时，可能面临以下一些问题：

• 首先我们需要定义测试用例之间的距离，这一距离的定义可能需要我们分析程序的具体规格说明；
• 我们还要考虑测试用例的分布情况，在随机测试中，测试用例在输入域当中的分布是均匀的，而自适应随机测试可能不满足这一需求。

当测试用例数量非常庞大时，人们发现大量的测试用例聚集于输入域的边界附近，为此人们提出了一种扩大输入域的自适应随机测试技术。首先人为扩大输入域之后，在这个扩大的输入域上使用自适应随机测试技术，这样大量的测试用例会聚集于扩大之后的边界上，之后我们将扩大的那部分数域剪切掉，这样在剩下的区域当中，测试用例的分布依然是均匀的。

3.5 反随机测试（Anti-Random Testing）

此前我们介绍了随机测试和自适应随机测试，我们发现不管是在随机测试还是自适应随机测试当中，我们所给的例子它都具有一个连续的输入域，那么在一个不连续的输入域上，我们又怎么样使用类似的方法？为此人们提出了 Anti-Random Testing 这样一种测试技术。

我们考虑这样一个程序，在这样一个程序当中，所有 8 个输入变量都是布尔类型，也就是说它们的取值只能是 0,1 两种情况。显然这一程序它的输入域是离散输入域：

bool TCAS7(bool a, bool b, bool c, bool d, bool e, bool f, bool g, bool h)
{
    return (a&&c || b&&d) && e && (f && g || !f && h);
}

对这一程序我们可以采用 Anti-Random Testing 的技术：

• 首先我们可以随机的选择第一条测试用例之后，我们在选择第二条测试用例时需要计算测试用例与此前已有的测试用例的海明距离之和
• 我们从所有可能的测试用例当中去选择这样一条测试用例，使得它与此前所有测试用例的海明距离之和最大
• 以此类推，直到我们找到错误或是测试资源耗尽。

在使用 Anti-Random Testing 的过程当中，我们看这样一个例子：

假设我们随机选择了第一条测试用例，在第一条测试用例中，所有的 8 个输入变量取值都为 0。那么在选择第二个测试用例时，我们可以选择所有 8 个变量，输入值都为 1 的测试用例，那么这条测试用例与此前那条测试用例它的海明距离是 8。

此后我们选择第三条测试用例时会发现：任意一条测试用例它与此前两条测试用例海明距离之和都是 8，这个时候我们不妨选择 test3 这样一条测试用例。之后再选择第四条测试用例时，我们发现 test4 这条测试用例它与此前三条测试用例的海明距离之和为 16 ，是所有测试用例当中最大的。以此类推，直到测试终止条件满足，这就是 Anti-Random Testing 的基本过程。

---

4. 组合测试

这一节我们来了解组合测试。在之前我们已经学习了几种黑盒测试技术，包括随机测试，等价类划分，边界值分析这几种测试技术，但是这些都没有考虑程序输入与输出之间的关系，这可能会导致测试效率相对低下。

那么为了解决这些问题，我们又介绍了决策表，决策表这一测试技术，有些人又把它归为基于模型的测试技术，它考虑了程序输入与输出变量之间的联系，并且准确地反映了这种关系。但这种方法存在的问题是使用起来比较复杂，因为提取输入变量与输出变量之间的联系是比较困难的。另一方面想要表达这种关系也比较困难，我们可能需要数量比较多的规则。

而另一方面，我们在进行测试时，可能还需要考虑不同的输入变量之间的联系。在传统的基于等价类的测试当中，假设有四个输入变量 A、B、C、D，分别做了等价类划分，那么我们在测试时只需要这么几条测试用例，保证每一个输入变量，所有的等价类在测试用例当中都出现至少一次就可以。但显然这种测试方法没有考虑不同输入变量之间取值的关系。

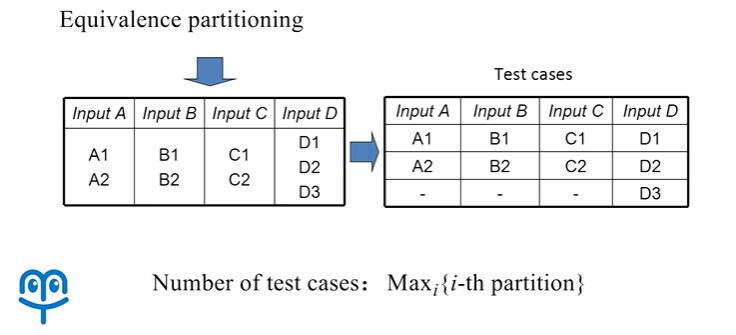
而事实上在很多软件当中，不同的变量之间，它们可能是协作工作的，例如可能某一个输入，它不能单独的决定输出，而一个输出可能是由多个输入共同所决定的。那么这个时候我们进行测试，就要考虑不同的输入变量之间的联系。又例如这样一个程序，计算 4 个变量开平方之和：

测试这一程序，我们显然需要考虑不同的变量之间的关系，要考虑不同变量取值之间的组合。如果我们要考虑这种取值之间的组合，那么最暴力的方法是进行完全组合。

例如对于 ABCD 这 4 个变量，我们分别等价类划分之后，进行完全组合测试，需要这么多测试用例：

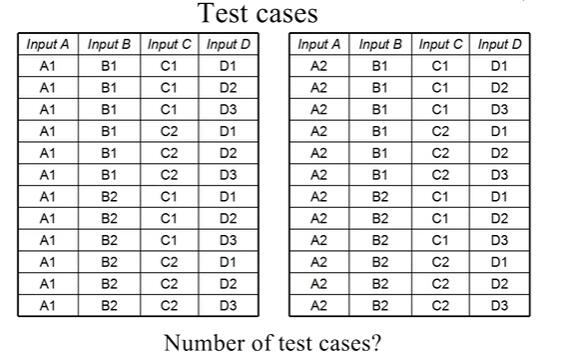
这个测试用例的数量等于每一个变量所拥有的等价类数量相乘的结果，显然测试代价是比较高的。很多时候我们没有办法进行这么暴力的测试，也没有办法拥有这么多的测试资源，只能在完全组合测试的基础上进行一个抽样。有一种最典型的抽样方法叫做两两组合测试（ Pair-wise testing）。那么在两两组合测试当中，我们可以令任意两个输入变量之间，所有的取值组合在测试用例当中都出现：

例如在这样一个测试用例表当中，我们可以看到，不管是 A,B 之间、A,C 之间、A,D 之间还是 B,C 之间、C,D 之间，所有的取值组合都是出现的：

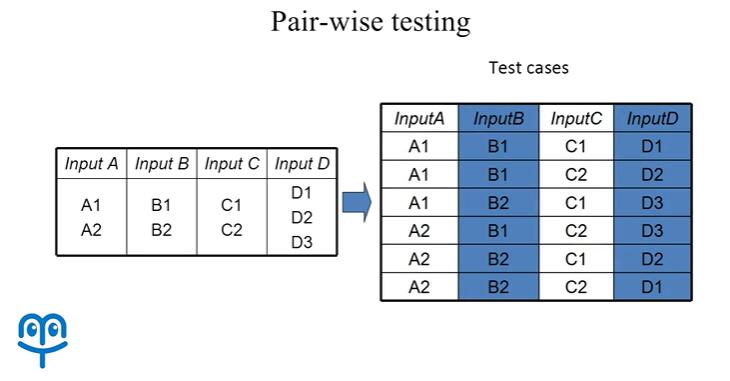
那么这种测试方法可以覆盖到任意两个变量之间，所有的取值组合，也就是说考虑到了任意两个变量之间可能存在的联系。那么对两两组合测试进行扩展，我们可以得到 T-wise 或者 T-way 的组合测试，例如我们令 t 等于 3，就可以得到这样一个三维组合测试用例集：

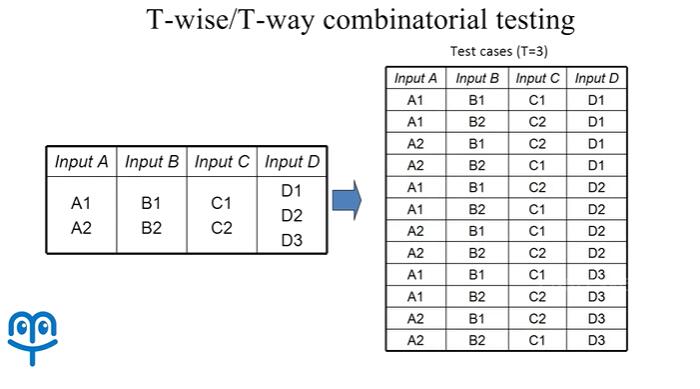
在这样一个测试用例集当中，任意三个输入变量之间，所有的取值组合都能保证出现。例如我们可以检查 B,C,D 三个输入变量之间，所有的取值组合数量是 12 组，在这个表当中都出现了。

之前所讲的 Pair-wise testing 和 T-way testing 都是对完全组合测试进行了一种抽样，而在之前的抽样当中，我们总是考虑任意相同数量的输入变量之间的联系，而在实际当中一个输出变量所涉及到的输入变量的数量可能是不同的。

例如对于某一个程序，我们通过分析可能会发现第一个输出变量受到 A,B,C 三个变量的影响，第二个输出变量受到 A,D 两个变量的影响，而第三个输出变量受到 C,D 两个变量的影响，这样的话我们对 A,B,C,D 不管是进行二维的组合测试，还是三维的组合测试，可能都是不合适的，这样我们可以使用可变粒度的组合测试，就是根据这种具体的关系来设计测试用例。

那么在这样一个可变粒度的组合测试用例当中，我们发现 A,B,C 之间所有的取值组合都被覆盖到，A,D 之间所有的取值组合都被覆盖到，C,D 之间所有的取值组合也都被覆盖到。那么其他两个或者多个变量之间的取值组合，我们不做考虑。

5. 组合测试中的默认取值问题

5.1 默认取值与基本选项测试

之前在介绍组合测试时，我们提到有些输入变量当中可能会存在一些需要我们特殊关注的情况，今天我们就介绍输入变量当中的默认取值。

大家都使用过微软的 office 软件，office 当中的 word 大家在使用时可以通过鼠标右键点击字体，得到这样一个菜单，在这样一个菜单当中，大家可以对中文以及西文字符选择字体，选择字号，选择不同的字符显示效果。大多数同学在使用 word 时并不会更改里面的内容，也就是说我们会使用默认的字体字号以及显示效果，可能会有 95%以上的同学以及用户在使用这一软件时都是这样使用的。也就是说对于软件当中的这些默认设置，我们可能需要进行比较多的测试。

下面我们介绍基本选项测试，假设 A,B,C,D 4 个输入变量通过等价来划分，得到了 A1,A2,B1,B2,C1,C2,D1,D2,D3 这样等价类列表。

那么在这样一个等价类列表当中，我们发现 A1,B2,C2,D3 是一组默认选项，也就是说程序大部分情况下都是在这一默认选项下工作的，那么在进行测试时，这样一个默认选项，我们是必须要进行测试的，我们把它作为第一条测试用例。

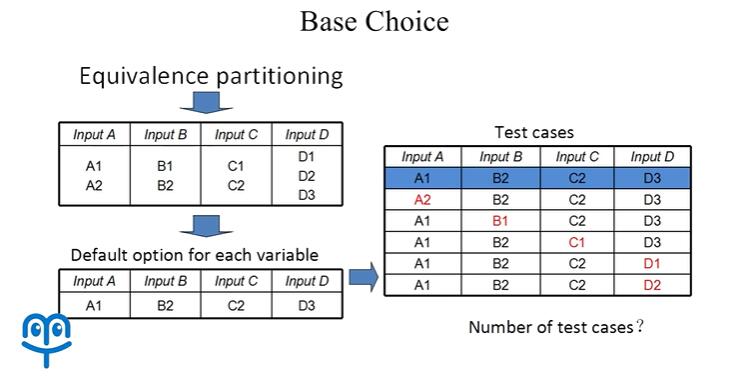
当然有些用户在使用这一软件时，可能会更改默认配置，而绝大部分用户在更改默认配置时，不会一次性的把所有配置都更改掉，他可能一次只更改其中的一个配置，那么所以我们在测试时可以在默认配置的基础上，每次更改其中的一条配置，直到满足等价类划分测试的要求,，如上图所示。

5.2 多重基本选项测试

除此之外，我们还需要考虑多重基本选项测试，同样是这样一个例子：

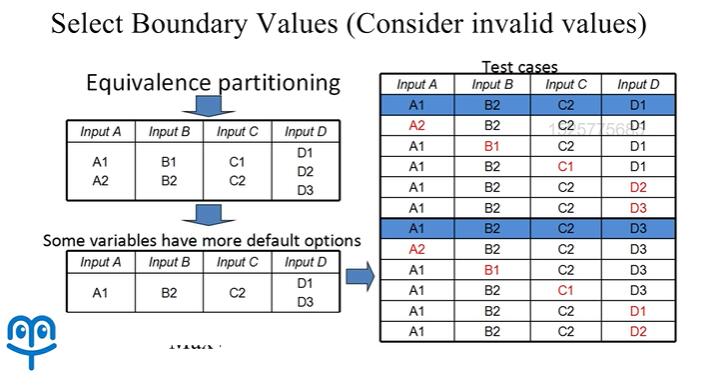
我们可能会发现对于 D 这样一个输入来说，D1,D3 都是默认配置，那这样我们在进行测试时需要考虑的默认配置就有两条。我们从这两条默认测试用例出发，分别使用基本选项测试的方法去扩展测试用例。最后再将这两组测试用例合并，就可以得到多重基本选项测试的测试用例。那么这样一组测试用例，一方面可以保证我们测试到基本选项，保证绝大部分用户的工作是正常的。另外一方面，对于少部分会去更改选项的用户，我们也能够保证他们的配置能够正常工作。

5.3 输入变量间的取值约束处理

之前我们提到在测试时要考虑不同输入变量当中可能具有的一些特殊情况，现在我们考虑不同输入变量可能存在的取值约束，大家看这样一个程序：

Bool Fun(bool a, bool b, bool c, bool d, bool e, bool f, bool g, bool h)
{
    if(a && !b)
        return false;
    return (a && c || b && d) && e && (f && g || !f && h);
}

在这样一个函数当中的第一行代码，我们看到当 a 取值为真，b 取值为假时，整个函数 return false，而此后的语句不会得到执行。

也就是说当 a,b 取值分别为真和假时，这样一条测试用例当中，其他的变量的取值是不会得到测试的。那么一方面我们需要专门针对 a 取真 b 取假这种情况设计一条测试用来测试它是否会返回 false。另外一方面我们还需要设计一些测试用例，回避掉 a 取真必取假的情况，以便能够顺利的测试其后的语句。那么这个时候 a 取真 b 取假的测试用例，我们要想办法回避，也就是说 a 取真 b 取假是这个函数当中可能存在的一个约束。

5.4 约束处理方法一：合并输入变量

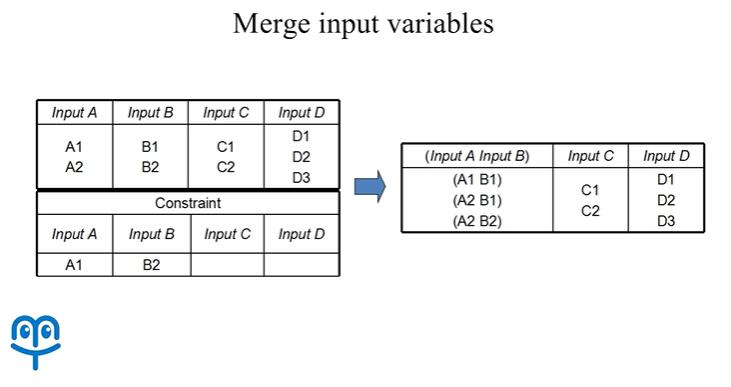
我们考虑之前进行等价类划分的这样一个输入模型，假设 A1,B2 是一组受到约束的取值，也就是说当变量 a 取 A1，变量 b 取 B2 时，测试用例的运行会直接失败。那么我们在设计测试用例时，在大部分情况下就要回避掉变量 a 取 A1，变量 b 取 B2 的情况。

为了解决这个问题，人们提出了一种合并输入变量的方法，例如我们可以将存在约束关系的 A,B 两个输入变量合并为一个输入变量，相应的，A,B 合并之后的输入变量，我们令它的取值包括 (A1 B1) (A2 B1) (A2 B2) 这三种情况，那么受到约束的 (A1 B2)，我们不再考虑，这样针对新的输入模型进行测试，我们就可以回避掉 (A1 B2) 这一受限的取值组合。

5.5 约束处理方法二：划分输入模型

针对这些问题，第二种方法我们也可以改造输入域模型，例如对于之前的输入域，现在我们可以切分成两个不同的输入域：

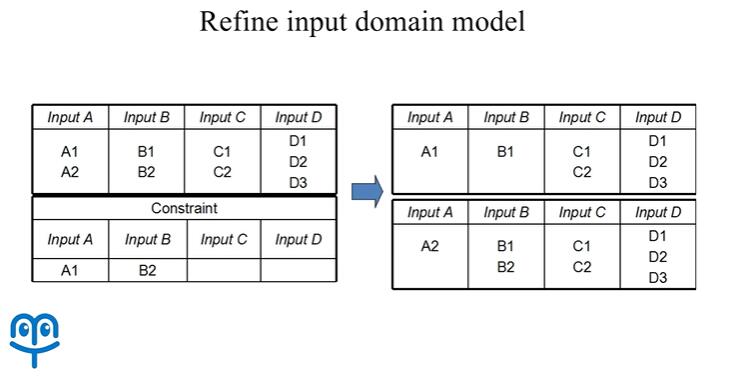
在这两个输入域当中，C,D 这两个输入变量保持不变，而 A,B 的取值情况发生了变化。在改造后的第一个输入模型当中，A 只有 A1 种取值，B 只有 B1 一种取值。很显然所有 a 等于 A2 或者 B 等于 B2 的取值都是不会出现的。而在改造后的第二个输入域模型当中，A 的取值有 A2，B 的取值有 B1,B2，那么很显然在第二个输入域模型当中，受限的情况也是不会发生的。

这样我们针对两个改造后的输入模型，分别设计测试用例，并将两组测试用例合并，就可以得到一组不包含受限取值的测试用例集合。

5.6 约束处理方法三：修改已有测试用例

那么最后假如我们此前的测试用例当中已经包含了受限的取值组合，那么我们也可以采用改造已有测试用例的方式来进行。假设我们已经有 A1,B2,C1,D1 这样一条测试用例，我们可以将这条测试用例拆分为两条不同的测试用例：

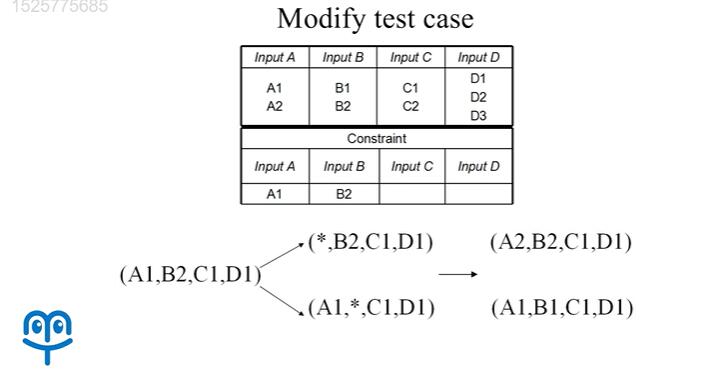
对于第一条测试用例，A 的取值置为空。对于第二条测试用例，B 的取值置为空。之后，我们将取值为空的位置分别用不受限的取值进行替代。在第一条测试用例当中，我们可以让 A 取 A2，在第二条测试用例当中，我们可以让 B 取 B1，这样原有的受限的 A1,B2 的取值不再出现，而其他的取值之间的组合则没有受到影响。