白盒测试入门系列(8) : 基于故障的逻辑测试
|
155
|
0
|

1458 字
|
6 分钟

1. 逻辑测试中的故障类型

1.1 弱变异测试

在上文中我们提到，变异测试往往需要较高的成本，所以后来人们提出了弱变异测试的概念。在弱变异测试中，如果测试用例在原始程序和变异体上执行后，程序中出现了不同的状态，也就是说某些变量或某些表达式具有了不同的值，我们就认为测试用例检测到了变异。

由于谓词语句中逻辑表达式在程序中所起的重要作用，人们往往会关注程序中逻辑表达式的状态变化。

1.2 面向操作符号的故障类型

在逻辑测试里面最常见的有 10 种故障类型，分别为有 4 种是面向操作符号的故障类型，有 6 种是面向操作数的故障类型。

我们针对以下的表达式先讲解 4 中操作符号类故障：
$$
E=(a | b) \& c
$$
OFF（Operator Fault）：操作符误用。譬如在原表达式 a or b and c 中，将 or 错误替换为 and，变成 a and b and c，即：
$$
E=(a | b) \& c
$$
ENF（Expression Negation Fault）：表达式误加否定。譬如某个子表达式被错误地加了一个 not 操作，即：
$$
E=!(a | b) \& c
$$

VNF（Variable Negation Fault）：变量误加否定。譬如原变量 c 被误写成 not c，即：
$$
E=(a | b) \& !c
$$
LOF（Lack of Parenthesis Fault）：优先级误用，常见为括号缺失，如：
$$
E=a | b \& c
$$

1.3 面向操作数的故障类型

操作数类故障有以下 6 种：

MVF（Missing Variable Fault）：漏掉操作数。譬如写 a or b and c ，遗漏了变量 c：
$$
E=(a | b)
$$
VF（Variable Fault）：变量误用。譬如本应为 c，却误写为 a：
$$
E=(a | b) \& a
$$
CCF（Clause Conjunction Fault）：多加 and 变量。譬如错误地加了 and a 形成 c and a：
$$
E=(a | b) \& (c \&a)
$$
CDF（Clause Disjunction Fault）：多加 or 变量，譬如错误地加了 or a：
$$
E=(a | b) \& (c|a)
$$
SA 0（Stuck-at-0 Fault）：变量“卡死”为 0：

$$
E=(0 | b) \& c
$$
SA 1（Stuck-at-1 Fault）：变量“卡死”为 1：

$$
E=(1 | b) \& c
$$

注：SA 0/SA 1 是来自于硬件的一种思想，因为在硬件制造当中很可能把某些节点给焊死，这时候这个通道可能永久为 0 或者 1。但这样一个故障在软件里面依然有它的意义，假如程序里有某个布尔函数误写了，很可能整个布尔函数永久的为 0 或永久的为 1。

2. 故障类型的强弱

2.1 故障类型强弱关系的概念

基于 10 种逻辑故障类型，我们可以来定义故障类型之间的强弱关系。

我们说一个故障类型 $F_A$ 比另外一个故障类型 $F_B$ 强，是指 $F_B$ 里面任意一个故障，我们都能在 $F_A$ 里面找到一个对应的故障。即FB 中所有故障在 FA 中都有对应的故障。

很难以理解对吗，没关系，我们可以通过测试用例集的集合的定义来表达这种概念。

  • 用 K(f, e) 表示能杀死关于表达式 e 的故障类型 f 的所有测试用例集合。
  • T ⊆ K(f, e) 表示测试集 T 是能杀死该故障的所有测试用例的子集（即 T 可能没有完全覆盖所有能杀死该故障的用例）
  • 若 K(FB) ⊆ K(FA)，则称 $F_A$ 强于 $F_B$

举个例子，假设：w

  • 杀死 FB 需要测试用例集合 A
  • 杀死 FA 需要测试用例集合 A 和 B
    显然有 A ⊂ A ∪ B ，此时我们可以说 $F_A$ 强于 $F_B$。

2.2 10 种故障类型的强弱关系

Chen 等在 2011 年的文章《A revisit of fault class hierarchies in general Boolean specifications》中得出了这些故障类型的强弱关系：

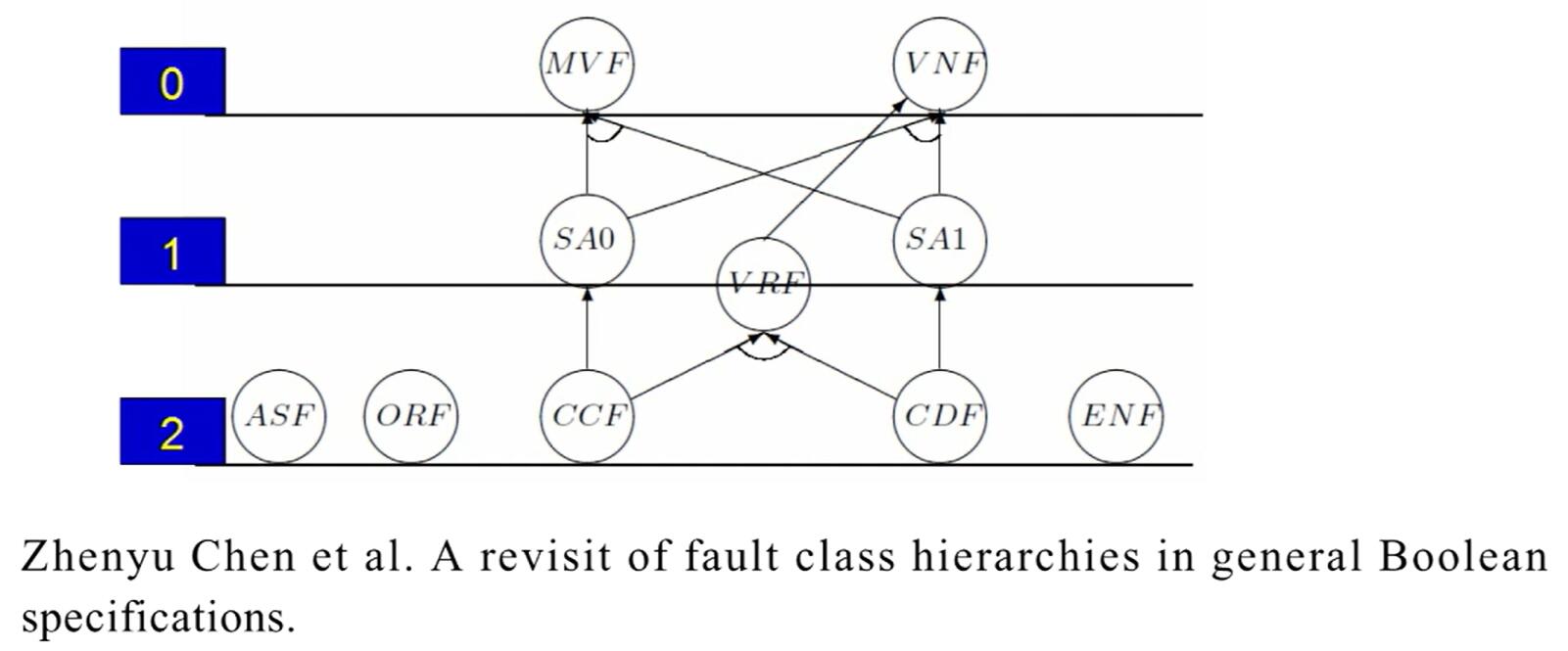
故障类型强弱关系图

最上层是最弱，我们称为第零层，中间为第一层，最下面最强为第二层。

我们以 level 1 以及 SA 0 和 SA 1 为一个测试覆盖目标来看这张图里面隐藏了什么，和我们之前介绍的逻辑覆盖又有什么关系：

MC/DC 与故障层级关系图

首先我们回顾一下 MC/DC 的概念，MC/DC 要求你这样做：

  • 只改变一个条件，比如 a
  • 其它条件不变，比如 b 和 c 不变
  • 看表达式 E 的结果有没有变

如果结果变了，就说明这个条件“单独起作用”了 → 满足 MC/DC。

关注表达式 E = (a|b) & c，我们利用 MC/DC 先来测试两组数据：

用例 a b c 结果 E = (a OR b) AND c
1 1 0 1 (1 OR 0) AND 1 = 1
2 0 0 1 (0 OR 0) AND 1 = 0

这个测试满足 MCDC 要求：a 的变化“单独”影响了结果。我们用 SA 0/SA 1 将 a 固化为 0/1，测试结果也是一样，我们发现：

✅结论： SA 0 + SA 1 ≈ MC/DC

不难发现 SA 0 + SA 1 就是我们的 MC/DC 测试，而刚才我们测试分三层，SA 0 加 SA 1 只是中间的一层，在实际操作当中，我们可以根据测试等级要求，采用比较浅的 level 0 的测试标准，或者采用更加强的 level 2 的测试标准来构造不同强弱的逻辑测试。